別の記事にて期待効用理論について紹介し、その矛盾をつくアレのパラドックスについても説明してきました。これによって期待効用理論は更なる改変が求められることとなるのです。
ここでトヴェルスキーとカーネマンが「プロスペクト理論」を提案することとなります。今回はこのプロスペクト理論について解説していきたいと思います。
プロスペクト理論の概観
先に述べたように、プロスペクト理論はアレのパラドックスで見つかった期待効用理論の矛盾を克服する理論になります。そこには2つの大きな柱があり、その2つの柱によって理論が成立しています。「価値関数」と「確率ウェイト関数」の2つです。
期待効用理論では以下のような数式が存在しました。初期保有を\(e\)、ある金額を持っている時の効用を\(u(g)\)とする。そして、確率変数を\(X\)、その確率を\(P\)とした時の期待効用\(E(u(e + X))\)は、
$$ E(u(e +X)) = \sum_{i=1}^{m}{P_iu(e + X_i)} $$
つまり、確率と確率変数が中心となっていたわけです。そして、プロスペクト理論においてもそれら2つが中心であることは変わりません。しかし、それぞれにあった問題点を再認識し、修正を加えたものが必要とされたのです。それこそが「価値関数」と「確率ウェイト関数」になります。
まずはそれぞれについて紹介し、その2つからなぜプロスペクト理論が成立するかを見ていきましょう。
僕は一橋大学大学院の経済学研究科で行動経済学について研究していました。経済学の面白さ、社会での有用性を広げるため、当ブログを開設しました。
このブログ(Economix)では経済学と大好きなガジェットを中心に情報発信しています。
価値関数
まずは価値関数について見ていきましょう。価値関数は期待効用理論で言うところの確率変数に当たるものです。期待効用理論では確率でもらえる金額に対する効用を確率変数としていました。その際、初期費用\(e\)を考慮した\(u(e+X)\)が確率変数の数式です。しかし、価値関数ではそれを変更しようと言うのです。
ここからは、経済学での「効用」と似ているものの、実質的には異なる「価値」という概念を考えます。効用では「満足度」をもとにしていましたが「価値」ではその金額にどれだけの価値が自分にあるかを主眼に捉えます。とはいえ、ややこしい話なので、価値関数では効用ではなく価値と呼ぶんだなくらいで大丈夫です。
さて、価値をどのように測るのでしょうか?期待効用理論では初期保有へのプラスマイナスに対する効用を考えていました。価値関数ではここが大きく変わります。現在持っている金額、つまり初期保有を原点と考えるのです。この原点のことを「参照点」と呼びます。初期費用から「どれだけ増えるのか・減るのか」で価値を測ろうということです。
そして、人々の価値のおき方を観察してみると以下のような性質があることが明らかとなったのです。まずはプラスに関してです。人は得をするともちろん喜び、そこに価値を置きます。しかし、もらえる金額が多くなるにつれ、そこにおく価値の伸び率がどんどん減っていくのです。
一方、損失局面ではどうでしょうか?損をするとなると嫌な気分つまり価値をマイナスに捉えます。そして、損が少し増えただけでもかなり損した気分になります。5万円もらう喜びより5万円失う悲しみの方がかなり大きいですよね?つまり、損失に対して価値の減りはどんどん大きくなっていくのです。
こうした価値関数への人々の振る舞いをグラフに表すと以下のようになります。原点の部分が参照点です。そして、利得に対する価値関数の伸びは大きくない一方、損失に対する目減りは大きいのです。ここでは、利得をXとして、価値をv(X)として表しています。
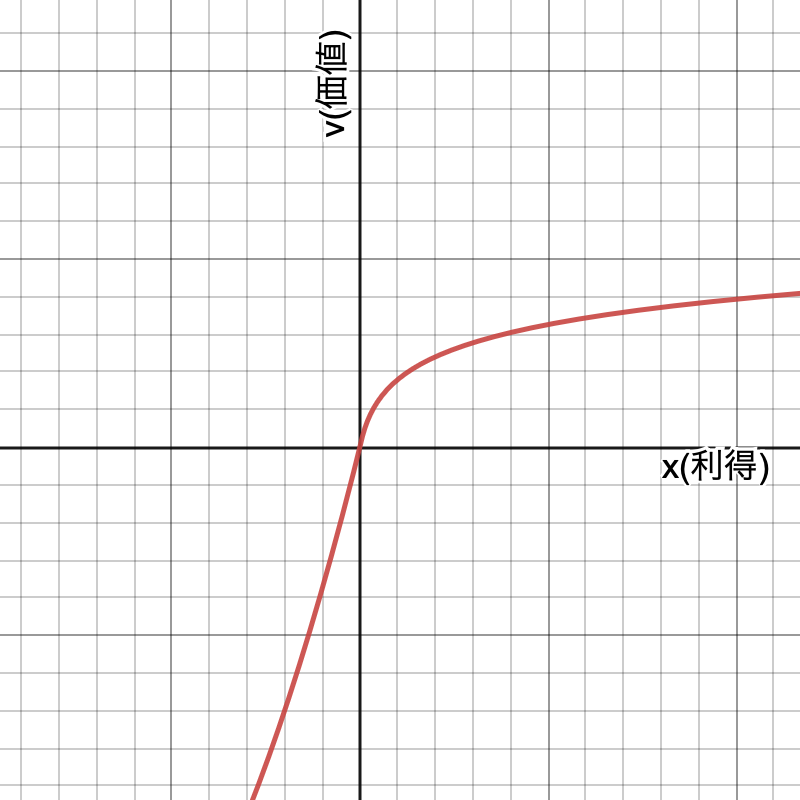
余談となりますが、これを価値に対する期待値(仮に期待価値とでも呼びましょう)と比較するとどうでしょうか?利得局面では通常より価値を低く見てしまうのでリスクプレミアムは大きくなっており、危険回避性を持っているといえるでしょう。一方で、損失局面では価値の目減りが実際よりも大きくなっています。つまり、危険愛好的になっているといえます。
確率ウェイト関数
ここまで価値関数を見てきました。ここからはもう1つの柱「確率ウェイト関数」について見てみましょう。価値関数が確率変数に対応していたのですから、確率ウェイト関数は確率に相当するものです。名前に確率とあるので一目瞭然ですが、、、。
では確率ウェイト関数とは何なのでしょうか?名前に「ウェイト」とあるように、確率に対する重み付けです。人間は無意識のうちに勝手に重み付けを行い、実際の確率とは異なる確率を自分の中で生み出してしまうのです。エルスバーグパラドックスのように人間は正しく確率を評価することができないのです。
ここではトヴェルスキーとカーネマンが観察によって見出したウェイト付について紹介しましょう。これまで確率を\(P\)としてきましたが、ウェイト付をした確率を\(w(P)\)としましょう。まずは極端な場合から見ていきます。確率が0や1については「絶対そうならない/なる」を表すものなので、ウェイト関数においても\(w(0)=0, w(1)=1\)となります。しかし、その中間地点はまちまちな振る舞いをするとされています。
確率が1から少し目減りすると、人は通常よりも確率が低いと考えてしまうというのです。「もしかしたら外すかもしれない」という考えが頭について回るということですね。一方で、0から少し増えると「ワンチャンあるかもしれない」と期待し、通常よりも確率を高く算定してしまうようです。こうした0や1から離れた部分で評価の誤りが大きくなることを「確実性等価」といいます。つまり、0付近においては\(w(P)>P\)となり、1付近では\(w(P)<P\)となるということですね。
では、これが入れ替わる点はどこなのでしょうか。正確なことは人や状況によりけりなので何ともいえませんが、彼らの実験においてはおおよそ\(P=0.4\)周辺で\(w(P)=P\)になるとされています。そして、もう1つ「劣確実性」という概念も示されています。当たり前ですが、\(P + (1-P) = 1\)となるものです。しかし、ウェイト関数においてはそれは満たされず、\(w(P) + w(1-P) < 1\)となることが示されているというのです。
これらを踏まえてグラフに表すと以下のようになります。
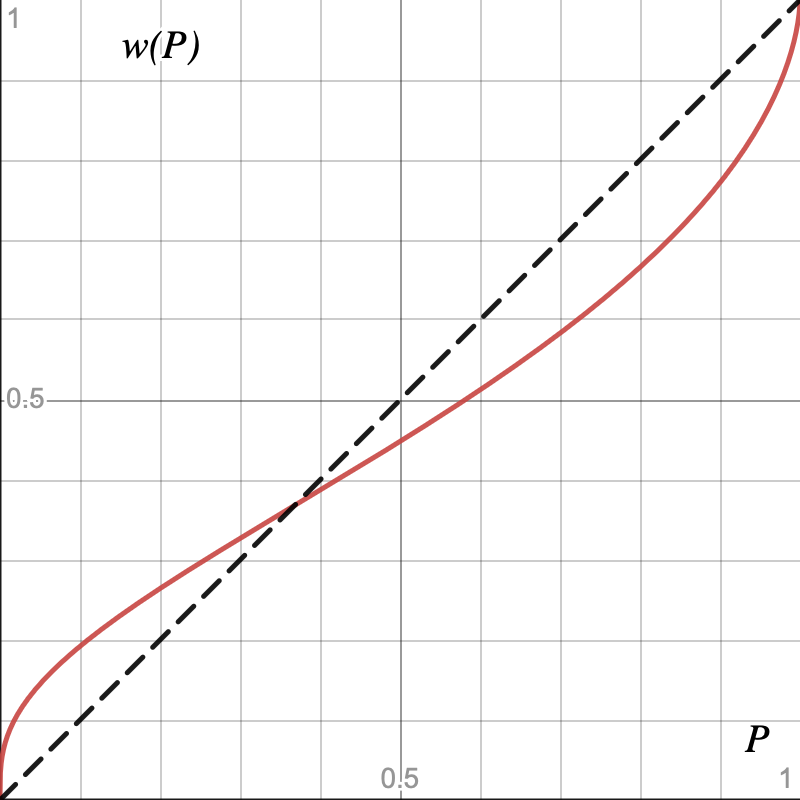
グラフの破線はウェイト関数が実際の確率と一致している\(w(P)=P\)の場合を表しています。グラフからも\(P<0.4\)の局面では実際の確率よりも高い確率を想定しており、逆に\(P>0.4\)の局面では低く見積もっていることが見て取れると思います。
プロスペクト理論
さて、これまでプロスペクト理論を構成する2つの柱「価値関数」と「確率ウェイト関数」を見てきました。それぞれ、確率変数や確率への人間の評価には歪みやずれがあり、それを踏まえた関数となっています。
ここで、期待効用理論のように数式に落とし込んでみましょう。価値関数は\(v(X)\)で確率ウェイト関数を\(w(P)\)とした時、
$$ w(P_1)v(X_1) + w(P_2)v(X_2) \dots + w(P_m)v(X_m) = \sum_{i = 1}^{m}{w(P_i)v(X_i)} $$
という形で期待価値を表すことができます。これがプロスペクト理論です。では、最後にこの理論がどのようにアレのパラドックスを克服したのかをみていきましょう。
まずはアレのパラドックスの説明に用いた4つのくじを再喝します。
<実験1>
A:確実に10億フラン貰える。
B:1%の確率で0フラン、10%の確率で50億フラン、89%の確率で10億フランが貰えるくじ
このどちらかの選択肢が与えられた際、多くの人はAを選択しました。
<実験2>
C:11%の確率で10億フラン、89%の確率で0フランが貰えるくじ
D:10%の確率で50億フラン、90%の確率で0フランが貰えるくじ
この場合では、多くの人がDを選択しました。
ではこの選好をプロスペクト理論に当てはめてみましょう。
実験1:\( v(10億) \succ w(0.01) \times v(0) + w(0.1) \times v(50億) + w(0.89) \times v(10億) \)
実験2:\(w(0.11) \times v(10億) + w(0.89) \times v(0) \prec w(0.1) \times v(50億) + w(0.9) \times v(0) \)
アレのパラドックスの時と同様に整理してあげると
実験1:\( (1 – w(0.89)) \times v(10億) \succ w(0.1) \times v(50億) \)
実験2:\(w(0.11) \times v(10億) \prec w(0.1) \times v(50億) \)
この2つの式が同時に成り立つ時はどのような時でしょうか?両方とも右辺は全く同じです。つまり、左辺の関係性に着目して、\(1 – w(0.89) > w(0.11) \)が満たされれば良いのです。ここで思い出してほしいのが「劣確実性」です。\(w(P) + w(1-P) < 1\)ってやつです。劣確実性の式に\(P=0.89\)を代入してあげると、
$$ w(0.89) + w(0.11) < 1 \Leftrightarrow 1 – w(0.89) > w(0.11) $$
つまり、矛盾は生じていないというわけです。以上のように、プロスペクト理論を導入することによってアレのパラドックスは克服され、人々の選好を表すことができるようになりました。
ただ、この理論においてもいくつかの問題点があることが示されています。それについてはまたいつかの機会に触れていきたいと思います。
まとめ
ここまでプロスペクト理論の成り立ちとアレのパラドックスの克服をご紹介してきました。プロスペクト理論には「価値関数」と「確率ウェイト関数」の2本の柱があり、それぞれを用いることでプロスペクト理論が構成されています。また、確率ウェイト関数を実装する際に見えてきた「劣確実性」をうまく活用することでアレのパラドックスは克服されたのです。
まだまだ人々の選好を正しく把握することはできていません。しかし、このように地道な実験や分析を繰り返し、数式を改良することでパラドックスを1つずつ解消していくのです。これこそが伝統的経済学から「より人に寄り添った」行動経済学への流れの特徴なのではないでしょうか?
今後もさまざまな実験や分析が進められ、このような大きな理論が樹立されるでしょう。それを楽しみに勉強を続けていきたいと思います。





