※当サイトはアフィリエイト広告を利用しています
前回は、「限界効用」と「消費者の選択行動」について学びました。
今回は、もう一歩進んで、「予算」という制約の中でどうやって最適な選択をするのかを考えます。
大学の経済学入門でも必ず出てくる「予算制約」と「無差別曲線」、そしてその交点である「最適消費点」について見ていきます。
名前は難しそうですが、実はとても日常的な考え方です。
今回は2財(例えばおにぎりとジュース)のみの簡単な経済を考え、直感的に理解できるように解説していきます!
(※実際の経済では財は無数にありますが、今回は基本を押さえるため2財に絞ります。)
僕は一橋大学大学院の経済学研究科で行動経済学について研究していました。経済学の面白さ、社会での有用性を広げるため、当ブログを開設しました。
このブログ(Economix)では経済学と大好きなガジェットを中心に情報発信しています。
予算制約とは?
まず、予算制約とは何なのかを見ていきましょう。
予算制約とは、一言で表すと「使えるお金の範囲内で購入できる商品やサービスの組み合わせ」を表すものです。
例えば、あなたが今、500円を持っていて、おにぎり1個100円、ジュース1本150円の場合について考えましょう。
このとき、購入できる組み合わせは限られていますよね。数式で表すと、
$$ 100x+150y≤500 $$
ここで、\(x\)はおにぎりの数、\(y\)はジュースの数を表しています。
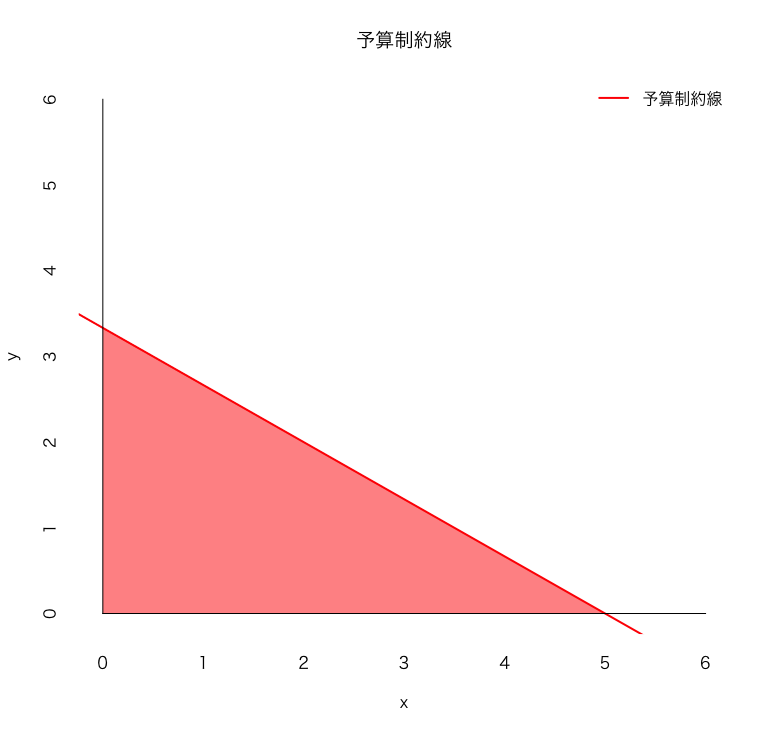
この制約式が「予算制約線」を決めます。グラフに描くと、直線になります。
直線の上にある点は「ちょうど予算を使い切る組み合わせ」、線より下の点は「お金が余る組み合わせ」です。
無差別曲線とは?
次に、「無差別曲線」について説明します。
無差別曲線とは、「消費者にとって満足度(効用)が同じ組み合わせをつないだ曲線」のことです。
例えば、おにぎり3個+ジュース1本の満足度と、おにぎり1個+ジュース2本の満足度があなたにとって同じであるとしましょう。
こうした、同じくらいの満足度である組み合わせを結んだ線が「無差別曲線」です。
数式で簡単な形を書くと、たとえば効用関数が \( U(x,y)=x ^α \times y ^ β\)のようになっているとします。
もし同じ満足度であるのであれば、\(x\)や \(y\)の数(\(α\)や\(β\))の組み合わせが変わろうが、 \(U(x,y)\)の結果は変わりません。
グラフに描くと、右下がりで「下に凸」なカーブになります。
たくさんおにぎりを持っているなら、ジュースが少なくても満足、という考え方ですね。
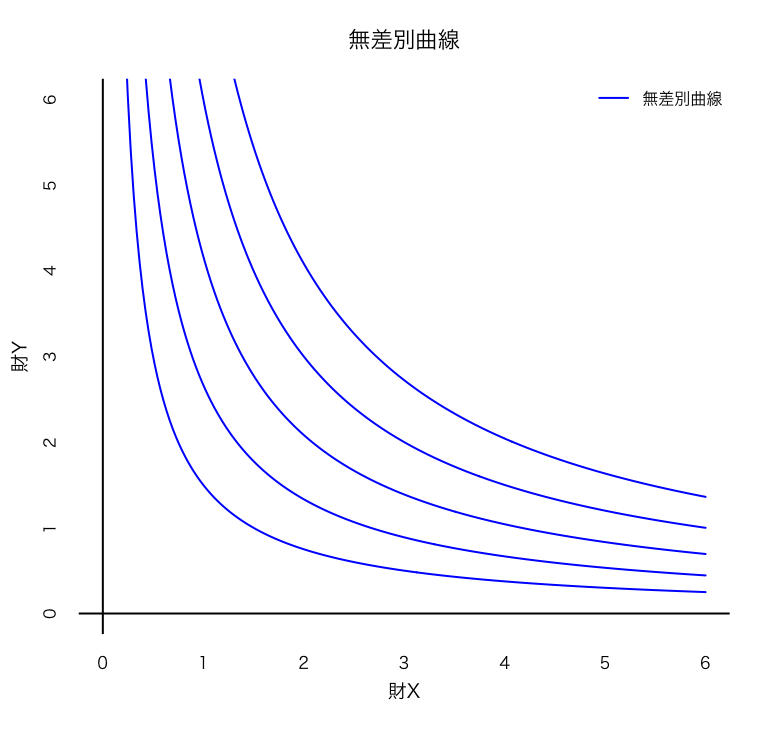
満足度が変われば、無差別曲線も変わってきます。そのため、2つの財に対して無差別曲線は無数に引くことができるのです。
そして、おにぎりとジュース1つずつの時よりも、それぞれ5つずつもらえる方がもちろん満足度が高くなっていきます。
そのため、無差別曲線が原点よりも外側(右上の方向)に存在しているものほど、高い満足度を表しているということができるのです。
最適消費点とは?
ここまでで、予算制約線と無差別曲線について見てきました。
では、実際にどの組み合わせを選ぶのが一番いいのでしょうか?
もちろん、お金を使い切りながら、最大限満足できる点で買い物できればベストです。
それは予算制約線と無差別曲線が接する点として捉えることができます。
お金を使い切るという観点から、まずは予算制約線上の点がベストであると分かります。
そうでなければ、お金が余ってしまいますからね。
そして、効用が大きい無差別曲線はなるべく右上のものです。では、予算制約線上を通って、なるべく右上の無差別曲線はどれか、辿っていくと接しているものであると気づくはずです。
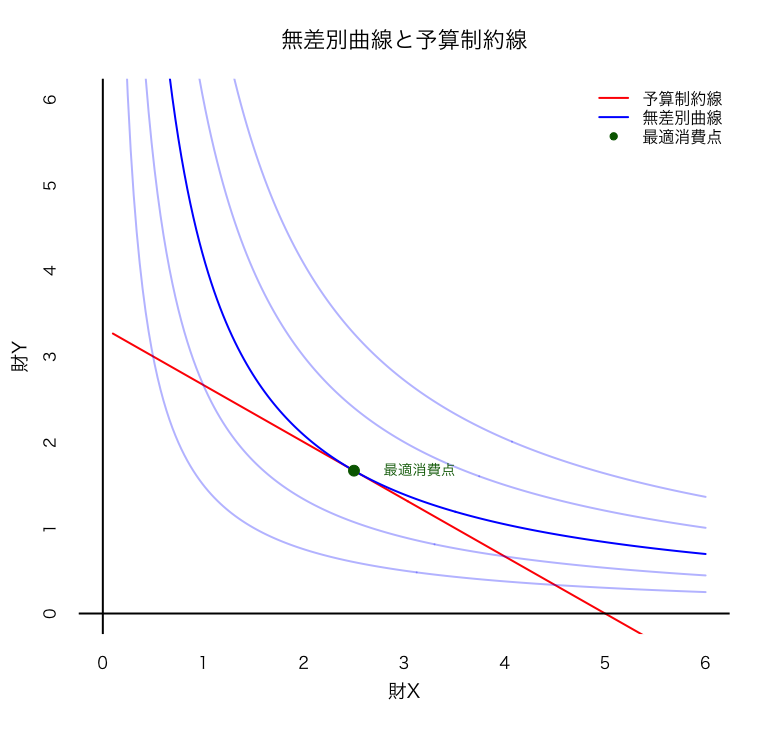
このとき、図を見ればわかるように、無差別曲線の傾きと予算制約線の傾きが等しくなっています。
式で表すと、限界代替率 \( (MRS)=\frac{P_x}{P_y} \)となります。
限界代替率\(MRS\)とは、ジュースを1本減らしたときに、おにぎりを何個増やさないと満足度が保てないかを表します。ちなみに、\(P_x\)はおにぎりの価格、\(P_y\)はジュースの価格を一般化して表したものです。
そして、\(MRS\)が予算制約線の傾きと等しくなった点が、最適消費点というわけです。
実社会ではどうなる?
今回は説明をわかりやすくするために2財(おにぎりとジュース)だけを考えましたが、
実際の生活では、食べ物、服、家賃、スマホ代…など、何十、何百もの財を同時に選んでいます。
この場合、予算制約式や無差別曲線も多次元になり、数式やグラフでは非常に複雑になります。
3財まではグラフで表せますが、4財以降は視覚化もままなりません。
しかし、基本的な考え方は全く同じです。
「使えるお金の範囲で」「できるだけ満足度を高める」という2点を意識している限り、理論は変わりません。
ミクロ経済学では、こうした単純なモデルから現実世界を理解する力を養っていきます。
まとめ
今回は、予算制約と無差別曲線から最適消費点を算出して、最適な消費とは何かを見てきました。
この考え方を押さえておくと、次回以降に学ぶ「需要の価格弾力性」や、もっと発展的な理論にもスムーズに進めます。
引き続き一緒にミクロ経済学を楽しく学んでいきましょう!

