みなさんは「フレーミング効果」という言葉を聞いたことがありますか?これは行動経済学の理論の1つであり、この効果によって人々の価値判断に変化が生じます。
今回はこの理論についてご紹介し、人々の認知にどれほど歪みが出ているのかを見ていきたいと思います。どう伝えるかだけで印象が大きく変わるという話なので、日常でも十分に使える知識になると思います!
僕は一橋大学大学院の経済学研究科で行動経済学について研究していました。経済学の面白さ、社会での有用性を広げるため、当ブログを開設しました。
このブログ(Economix)では経済学と大好きなガジェットを中心に情報発信しています。
リスク選好について
フレーミング効果について説明を始める前にリスク選好という概念を軽く説明しておきたいと思います。フレーミング効果を理解する上で基礎となる部分になります。
リスク選好とは端的にいうと「リスクがある選択肢とリスクのない選択肢を与えられた時、どちらを選ぶのか」という考え方になります。ここでいうリスクとは、基本的に確率的に結果が決定されるものと考えてもらって差し支えありません。
行動経済学ではリスクのある選択肢を選びがちな場合を「危険愛好」的と表現し、リスクのない安全な選択肢を選びがちな場合を「危険回避」的と表現します。
リスク選好についてはこの他に「確率等価」や「リスクプレミアム」という概念があるのですが、フレーミング効果を理解する上ではひとまず置いておいて良いでしょう。
リスク選好についてはこちらの記事で詳細を解説しているのでぜひ読んでみてください!フレーミング効果の理解もグッと深まると思います。
プロスペクト理論について
リスク選好に関して、プロスペクト理論についても少し触れておきましょう。これも後の議論の肝となるお話になります。
プロスペクト理論とは先に見たリスク選好を上手く含んだ、物事の価値評価に関する関数といったところでしょうか。ざっくり言うと、人々のものの評価にはリスク選好による歪みがあり、それはものの「価値」そのものと「確率の評価」に表れてきます。
価値については「価値関数」というもので表され、確率の評価は「確率ウェイト関数」によって表されます。
今回は価値関数について軽く知っていればわかるので、こちらのみご紹介します。
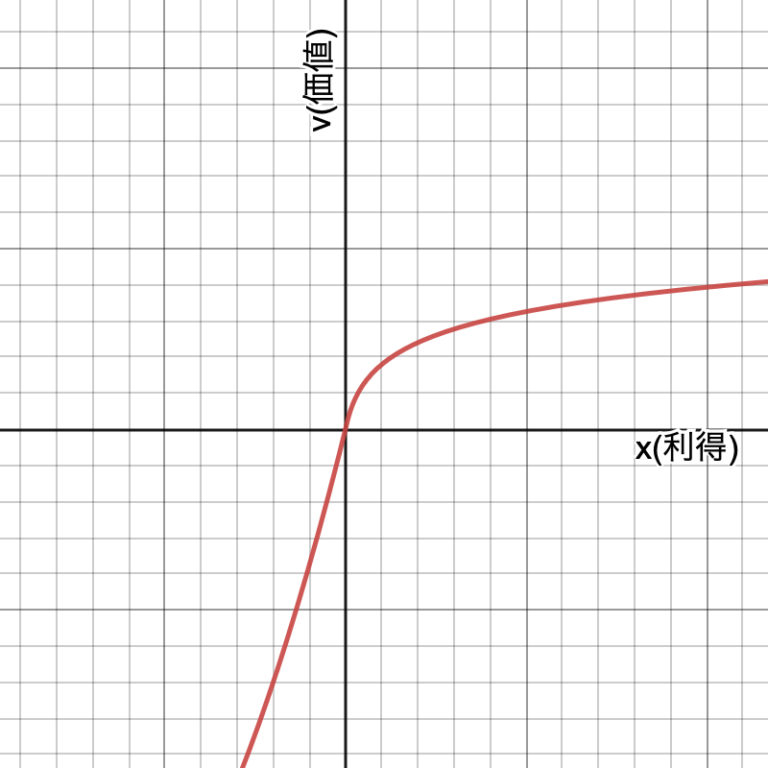
上のグラフが価値関数を表したものです。X軸の「利得」がものの本来ある価値、つまり値段などです。負の方向では「損失」と呼ばれます。そして、この利得や損失を人間は自身の基準によって「価値」という形で評価を行います。
グラフの形を見てもらうと、利得局面では、本来の価値よりも低く見積もっていることがわかるでしょう。一方、損失局面では本来の損失よりも多く損した気分になっています。
そして、プロスペクト理論では利得局面では「危険回避的」であり損失局面では「危険愛好的」であることが示されています。
今回は必要な部分のみをかい摘んだ解説となっています。本質的なプロスペクト理論については以下の記事で解説しているので参考にしてみてください。
フレーミング効果とは
リスク選好について知っておいてほしい部分は解説しましたので、ここからはフレーミング効果を見ていきましょう。フレーミング効果を端的に表すと「同じ内容でも伝え方1つで人々の意思決定に影響を及ぼす」というものです。
ではまず、フレーミングとは何でしょうか?フレームと聞くと窓枠とかの「枠」を表す言葉を想像するのではないでしょうか?行動経済学でも「枠」を表しているのですが、どのような「型」で話すのかといったニュアンスになります。
フレーミング効果の例①
ここでは初めに例を見ていきましょう。
ある製薬会社では2種類の薬を開発しており、どちらも同じ病気に対して作用するものです。この病気は治らなければ死に至ってしまうものとしましょう。
現在1200人がこの病気を患っており、Aの薬を使うと400人が治ります。Bの薬を使うと、3分1の確率で1200人が治るが、3分の2の確率で全員が亡くなります。
A:400人が治る
B:3分1の確率で1200人治るが、3分の2の確率で全員が亡くなる
ここで、あなたか周囲の人がこの病気に罹っていると仮定しましょう。そして、どちらの薬を服用するかの選択はあなたに委ねられています。あなたならA,Bどちらの薬を選びますか?
こうした問題が与えられた際、行動経済学ではAの薬を選ぶ人が多いことが認められています。多くの人が「400人も治るんだからこっちの方が良いんじゃないか?」「Bを選ぶと治るのは確率の問題か」と考えるようなのです。
しかし、ここでA,Bについてもう一度考え直して見ましょう。
Bの期待値を計算してみると、
$$ \frac {1} {3} \times 1200 + \frac {2} {3} \times 0 = 400 $$
つまり、AもBも全く同じことを言っているということです。
にも関わらず、A,Bを選択する割合は無差別(同じ)ではなくAが多くなってしまうのです。
Aの薬では「400人が治る」という確実な値が示されています。一方でBでは「3分の1」という確率が与えられている状態です。そして、「治る」という「利得」に注目した評価なのでプロスペクト理論の価値関数でいうところの第1章限での議論となるわけです。
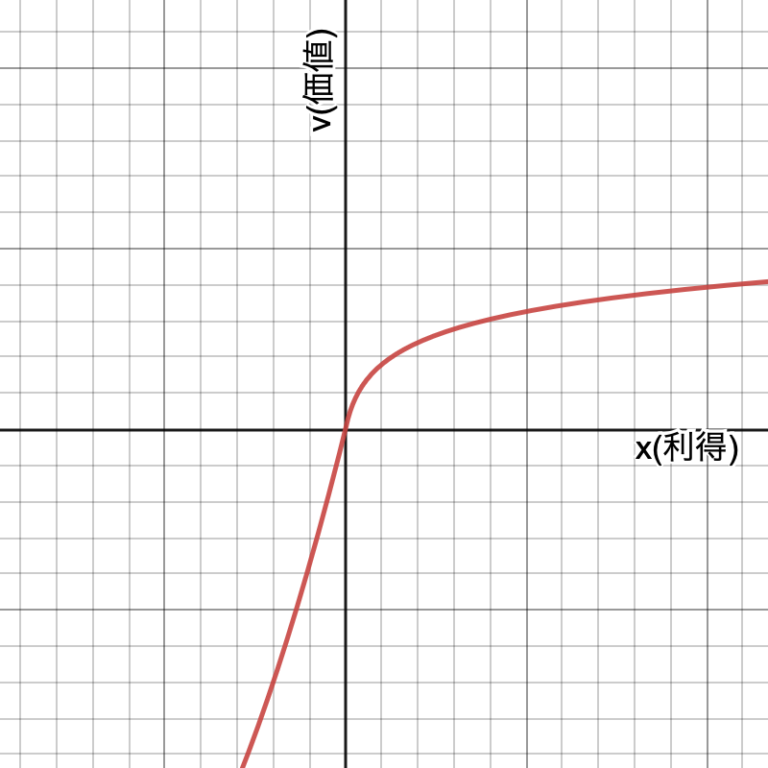
すると、「危険回避」的な行動が多く見られるのは納得ではないでしょうか?
フレーミング効果の例②
では同じ仮定をおいて、新しくA,Bの薬を設定しましょう。
Aの薬を使うと800人が亡くなります。Bの薬を使うと、3分の1の確率で全員が治るが、3分の2の確率で1200人が亡くなります。
A:800人が亡くなる
B:3分の1の確率で全員治るが3分の2の確率で1200人亡くなる
さて、今回はどちらを選びますか?
この問いが与えられた際はBを選ぶ人が多いことが行動経済学では認められています。ここでは「Aでは確実に800人も亡くなるのか」「Bでは亡くなるのは確率の問題か」と考えるようです。
ここでもう一度Bの期待値を計算してみましょう。ちなみに、Aでは\(1200 – 800 = 400 \)人の方が救われます。
$$ \frac {1} {3} \times 1200 + \frac {2} {3} \times 0 = 400 $$
そうです。例①の時と全く同じ状況を表しています。しかし、得られる結果は真逆。例①では危険回避的な選好が認められたにも関わらず、例②では危険愛好的選好が認められます。
先ほどと同様に見ていきましょう。
Aの薬では「800人が亡くなる」という確実な値が示されています。一方でBでは「3分の2」という確率が与えられている状態です。そして、「亡くなる」という「損失」に注目した評価なのでプロスペクト理論の価値関数でいうところの第3章限での議論となるわけです。

すると下に凸のグラフとなる訳ですから、危険愛好的と言えるのではないでしょうか?
まとめ
ここまでフレーミング効果について2つの例をご紹介しました。全く同じ内容であっても①②という異なる伝え方をするだけで意思決定に大きな差が生まれたことを理解していただけたと思います。
一方は危険回避的、他方は危険愛好的となるわけです。プロスペクト理論の視点から見てあげると、例①は「治る」、つまり「利得」に着目しているので「危険回避的」になります。一方、②は「亡くなる」つまり「損失」に着目しているので「危険愛好的」になると捉えられます。
「言い方1つで人の捉え方は大きく変わる」というのがフレーミング効果です。日常生活でも言い方に気を遣うだけで受け取り手の感じ方は変わりますよね?数字や「損得」について論じる際はこのフレーミング効果を意識するだけで相手の感じ方も変わってくるのではないでしょうか?
フレームを調整することで人の意思決定に影響を与えることができるのであれば、ナッジの余地があり、社会厚生やビジネスへの応用を十分にできると思われます。
今回は概要のみの紹介でしたが、この可能性に興味を持った方はフレーミング効果についてもっと学んでみるのも良いかもしれませんね!





